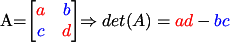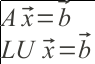Naomi Artama Silitonga: September 2018

A. PENGERTIAN DETERMINAN MATRIKS

Determinan matriks adalah sebuah angka atau skalar yang diperoleh dari elemen-elemen matriks tersebut dengan operasi tertentu.

Setiap matriks persegi atau bujur sangkar memiliki nilai determinan

Nilai determinan dari suatu matriks merupakan suatu skalar

Jika nilai determinan dari suatu matriks sama dengan nol, maka matriks tersebut disebut matriks singular

B. NOTASI DETERMINAN

Misalkan matriks A merupakan sebuah matriks bujur sangkar

Fungsi determinan dinyatakan oleh det (A)

Jumlah det (A) disebut determinan A

Det (A) sering dinotasikan |A|

C. NOTASI DETERMINAN

pada matriks 2x2 degan elemena a dan d terletak pada diagonal utama, sedangkan suatu b dan c terletak pada diagonal kedua

Contoh :

M=

5	2
4	3

det(M) =

5	2
4	3

= (5 × 3) – (2 × 4) = 7

Pada matriks 3x3 (pengayaan)

|A|=aC₁₁+bC₁₂+cC₁₃

|A|=a(ei-fh)-b(di-fg)+c(dh-eg)

METODE SARRUS

A =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

Contoh :

det(A) =

2	3	4
5	4	3
7	0	1

2	3
5	4
7	0

det(A) = 2.4.1 + 3.3.7 + 4.5.0 – 4.4.7 – 2.3.0 – 3.5.1

       =   8   +   63  +   0   –  112  –   0   –   15 
       = – 56

METODE LAPLACE

$E = \begin{bmatrix} 1&2&2&3&4\\ 4&9&10&13&17\\ 2&6&7&10&14\\ 3&10&20&22&40\\ 1&5&10&12&16 \end{bmatrix}$

Penjelasan :

$det(E) = \begin{vmatrix} 1&2&2&3&4\\ 4&9&10&13&17\\ 2&6&7&10&14\\ 3&10&20&22&40\\ 1&5&10&12&16 \end{vmatrix}$

$= a_{11}C_{11} + a_{21}C_{21} + a_{31}C_{31} + a_{41}C_{41} + a_{51}C_{51}$

$= a_{11} (-1)^{1+1} M_{11} + a_{21} (-1)^{2+1} M _{21} + a_{31} (-1)^{3+1} M _{31} + a_{41} (-1)^{4+1} M _{41} + a_{51} (-1)^{5+1} M _{51}$

$= a_{11} M_{11} -a_{21} M _{21} + a_{31} M _{31} -a_{41} M _{41} + a_{51} M _{51}$

$= 1\begin{vmatrix} 9&10&13&17\\ 6&7&10&14\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} -4\begin{vmatrix} 2&2&3&4\\ 6&7&10&14\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} + 2\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} -3\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 6&7&10&14\\ 5&10&12&16 \end{vmatrix} + 1\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 6&7&10&14\\ 10&20&22&40\\ \end{vmatrix}$

Selanjutnya, Karena

$M_{11}, M_{21}, M_{31}, M_{41}$ dan

$M_{51}$ merupakan determinan

$4 \times 4$ , maka kita uraikan lagi dengan menggunakan kofaktor. Ambil

$i = 1,2,3,4,5$ dan

$j=1$ .

$\begin{vmatrix} 9&10&13&17\\ 6&7&10&14\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} = 9\begin{vmatrix} 7&10&14\\ 20&22&40\\ 10&12&16 \end{vmatrix} -6\begin{vmatrix} 10&13&17\\ 20&22&40\\ 10&12&16 \end{vmatrix} + 10\begin{vmatrix} 10&13&17\\ 7&10&14\\ 10&12&16 \end{vmatrix} -5 \begin{vmatrix} 10&13&17\\ 7&10&14\\ 20&22&40 \end{vmatrix}$

Dengan menggunkaan Metode Sarrus, diperoleh

$= 9 \cdot 184 -6 \cdot 100 + 10 \cdot 12 -5 \cdot 138$

$= 1656 -600 + 120 -690$

$= 486$

$\begin{vmatrix} 2&2&3&4\\ 6&7&10&14\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} = 2\begin{vmatrix} 7&10&14\\ 20&22&40\\ 10&12&16 \end{vmatrix} -6\begin{vmatrix} 2&3&4\\ 20&22&40\\ 10&12&16 \end{vmatrix} + 10\begin{vmatrix} 2&3&4\\ 7&10&14\\ 10&12&16 \end{vmatrix} -5 \begin{vmatrix} 2&3&4\\ 7&10&14\\ 20&22&40 \end{vmatrix}$

Dengan menggunkaan Metode Sarrus, diperoleh

$= 2 \cdot 184 -6 \cdot 64 + 10 \cdot 4 -5 \cdot 0$

$= 24$

$\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} = 2\begin{vmatrix} 10&13&17\\ 20&22&40\\ 10&12&16 \end{vmatrix} -9\begin{vmatrix} 2&3&4\\ 20&22&40\\ 10&12&16 \end{vmatrix} + 10\begin{vmatrix} 2&3&4\\ 10&13&17\\ 10&12&16 \end{vmatrix} -5 \begin{vmatrix} 2&3&4\\ 10&13&17\\ 20&22&40 \end{vmatrix}$

Dengan menggunkaan Metode Sarrus, diperoleh

$= 2 \cdot 100 -9 \cdot 64 + 10 \cdot -2 -5 \cdot -48$

$= 200-576-20+240$

$= -156$

$\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 6&7&10&14\\ 5&10&12&16 \end{vmatrix} = 2\begin{vmatrix} 10&13&17\\ 7&10&14\\ 10&12&16 \end{vmatrix} -9\begin{vmatrix} 2&3&4\\ 7&10&14\\ 10&12&16 \end{vmatrix} + 6\begin{vmatrix} 2&3&4\\ 10&13&17\\ 10&12&16 \end{vmatrix} -5 \begin{vmatrix} 2&3&4\\ 10&13&17\\ 7&10&14 \end{vmatrix}$

Dengan menggunkaan Metode Sarrus, diperoleh

$= 2 \cdot 12 -9 \cdot 4 + 6 \cdot -2 -5 \cdot -3$

$= 24-36-12+15$

$= -9$

$\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 6&7&10&14\\ 10&20&22&40 \end{vmatrix} = 2\begin{vmatrix} 10&13&17\\ 7&10&14\\ 20&22&40 \end{vmatrix} -9\begin{vmatrix} 2&3&4\\ 7&10&14\\ 20&22&40 \end{vmatrix} + 6\begin{vmatrix} 2&3&4\\ 10&13&17\\ 20&22&40 \end{vmatrix} -10 \begin{vmatrix} 2&3&4\\ 10&13&17\\ 7&10&14 \end{vmatrix}$

Dengan menggunkaan Metode Sarrus, diperoleh

$= 2 \cdot 138 -9 \cdot 0 + 6 \cdot -48 -10 \cdot -3$

$= 276+0-288+30$

$= 18$

Jadi, diperoleh

$det(E) = 1\begin{vmatrix} 9&10&13&17\\ 6&7&10&14\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} -4\begin{vmatrix} 2&2&3&4\\ 6&7&10&14\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} + 2\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 10&20&22&40\\ 5&10&12&16 \end{vmatrix} -3\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 6&7&10&14\\ 5&10&12&16 \end{vmatrix} + 1\begin{vmatrix} 2&2&3&4\\ 9&10&13&17\\ 6&7&10&14\\ 10&20&22&40\\ \end{vmatrix}$

$= 1 \cdot 486 -4 \cdot 24 + 2 \cdot -156 -3 \cdot -9 + 1 \cdot 18$

$= 486 -96 -312 + 27 + 18$

=123

DETERMINAN : METODE CHIO

Perhatikan untuk matrik dengan ordo

$3 \times 3$ . Persamaan yang digunakan untuk metode CHIO ini sebagai berikut.

$det(A) = \dfrac{1}{(a_{11})^{3-2}} \begin{vmatrix} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{21} & a_{23} \end{vmatrix}\\ &\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{31} & a_{32} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{31} & a_{33} \end{vmatrix} \end{vmatrix}$

Selanjutnya untuk matrik dengan ordo

$4 \times 4$ . Persamaan yang digunakan untuk metode CHIO ini sebagai berikut.

$det(A) = \dfrac{1}{(a_{11})^{4-2}} \begin{vmatrix} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{21} & a_{23} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{14}\\ a_{21} & a_{24} \end{vmatrix}\\ &&\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{31} & a_{32} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{31} & a_{33} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{14}\\ a_{31} & a_{34} \end{vmatrix}\\ &&\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{41} & a_{42} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{41} & a_{43} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{14}\\ a_{41} & a_{44} \end{vmatrix}\\ \end{vmatrix}$

Apabila ukuran matriksnya diperluas atau diperumum menjadi

$n \times n$ , maka diperoleh persamaan untuk metode CHIO adalah sebagai berikut.

$det(A) = \dfrac{1}{(a_{11})^{n-2}} \begin{vmatrix} \begin{vmatrix} a_{11} & a_{12}\\ a_{21} & a_{22} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{21} & a_{23} \end{vmatrix} & \ldots & \begin{vmatrix} a_{11} & a_{1n}\\ a_{21} & a_{2n} \end{vmatrix}\\ &&&\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{31} & a_{32} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{31} & a_{33} \end{vmatrix} & \ldots & \begin{vmatrix} a_{11} & a_{1n}\\ a_{31} & a_{3n} \end{vmatrix}\\ &&&\\ \vdots & \vdots & \ddots & \vdots\\ \begin{vmatrix} a_{11} & a_{12}\\ a_{n1} & a_{n2} \end{vmatrix} & \begin{vmatrix} a_{11} & a_{13}\\ a_{n1} & a_{n3} \end{vmatrix} & \ldots & \begin{vmatrix} a_{11} & a_{1n}\\ a_{n1} & a_{nn} \end{vmatrix}\\ \end{vmatrix}$

Contoh 1.

Hitung determinan matriks

$A = \begin{bmatrix} -2&1&4\\ 3&-5&2\\ 5&2&1 \end{bmatrix}$ .

Dengan menggunakan metode CHIO, maka didapat

$det(A) = \dfrac{1}{(-2)^{3-2}} \begin{vmatrix} \begin{vmatrix} -2&1\\ 3&-5 \end{vmatrix} & \begin{vmatrix} -2&4\\ 3&2 \end{vmatrix}\\ &\\ \begin{vmatrix} -2&1\\ 5&2 \end{vmatrix} & \begin{vmatrix} -2&4\\ 5&1 \end{vmatrix} \end{vmatrix}$

$= \dfrac{1}{-2} \begin{vmatrix} (-5)(-2)-(3)(1) & (-2)(2)-(3)(4)\\ (-2)(2)-(1)(5) & (-2)(1)-(4)(5) \end{vmatrix}$

$= \dfrac{1}{-2} \begin{vmatrix} 7&-16\\ -9&-22 \end{vmatrix}$

$= \dfrac{1}{-2} (7 \cdot -22-(-16) \cdot -9)$

$= \dfrac{1}{-2} (-154-144)$

$= \dfrac{1}{-2} (-298)$

$= -149$

Contoh 2.

Hitung determinan matriks

$B = \begin{bmatrix} 2&1&6&7\\ 3&2&4&5\\ 4&4&2&3\\ 5&6&1&4 \end{bmatrix}$ .

Dengan menggunakan metode CHIO, maka didapat

$det(B) = \dfrac{1}{(2)^{4-2}} \begin{vmatrix} \begin{vmatrix} 2&1\\ 3&2 \end{vmatrix} & \begin{vmatrix} 2&6\\ 3&4 \end{vmatrix} & \begin{vmatrix} 2&7\\ 3&5 \end{vmatrix}\\ &&\\ \begin{vmatrix} 2&1\\ 4&4 \end{vmatrix} & \begin{vmatrix} 2&6\\ 4&2 \end{vmatrix} & \begin{vmatrix} 2&7\\ 4&3 \end{vmatrix}\\ &&\\ \begin{vmatrix} 2&1\\ 5&6 \end{vmatrix} & \begin{vmatrix} 2&6\\ 5&1 \end{vmatrix} & \begin{vmatrix} 2&7\\ 5&4 \end{vmatrix} \end{vmatrix}$

$= \dfrac{1}{2^2} \begin{vmatrix} (2)(2)-(3)(1) & (2)(4)-(3)(6) & (2)(5)-(3)(7)\\ (2)(4)-(1)(4) & (2)(2)-(4)(6) & (2)(3)-(7)(4)\\ (2)(6)-(1)(5) & (2)(1)-(6)(5) & (2)(4)-(7)(5) \end{vmatrix}$

$= \dfrac{1}{4} \begin{vmatrix} 1&-10&-11 \\ 4&-20&-22\\ 7&-28&-27 \end{vmatrix}$

Misal

$C = \begin{vmatrix} 1&-10&-11 \\ 4&-20&-22\\ 7&-28&-27 \end{vmatrix}$ , diperoleh

$det(C) = \dfrac{1}{1^{3-2}} \begin{vmatrix} \begin{vmatrix} 1&-10\\ 4&-20 \end{vmatrix} & \begin{vmatrix} 1&-11\\ 4&-22 \end{vmatrix}\\ &\\ \begin{vmatrix} 1&-10\\ 7&-28 \end{vmatrix} & \begin{vmatrix} 1&-11\\ 7&-27 \end{vmatrix} \end{vmatrix}$

$= \dfrac{1}{1} \begin{vmatrix} (1)(-20)-(4)(-10) & (1)(-22)-(-11)(4)\\ (1)(-28)-(-10)(7) & (1)(-27)-(-11)(7) \end{vmatrix}$

$= \begin{vmatrix} 20 & 22\\ 42 & 50 \end{vmatrix}$

$= (20 \cdot 50-22 \cdot 42$

$= 1000-924$

$= 76$

Jadi,

$det(B) = \dfrac{1}{4} det(C)$

$= \dfrac{1}{4} (76)$

$= 19$

DEKOMPOSISI MATRIKS DAN DETERMINAN

METODE CROUT

A = LDU A = LDU

being L a unit lower triangular matrix, D a diagonal matrix and U a unit upper triangular matrix, then Doolittle's method produces menjadi unit yang lebih rendah L matriks segitiga, matriks diagonal D dan U matriks segitiga atas satuan, maka metode Doolittle yang menghasilkan

A = L(DU) A = L (DU)

and Crout's method produces dan metode yang menghasilkan Crout

A = (LD)U. A = (LD) U.

METODE DOOLITTLE

Pada metode ini suatu sistem persamaan linier yang berbentuk:

difaktorisasi menjadi:

Pada dekomposisi LU metode Doolittle, semua komponen diagonal matriks L bernilai 1 sehingga representasi matriks di atas menjadi:

Untuk menghitung setiap komponen matriks L dan U dari matriks A dengan ukuran n x n dapat dengan menggunakan algoritma sebagai berikut:
1. Dapatkan nilai matriks U pada baris pertama:
untuk i = 1 sampai n