Naomi Artama Silitonga: RUANG VEKTOR

Sebelum memasuki materi utama, berikut ini adalah kompetensi dasar yang seharusnya sudah dikuasai pembaca:
1. Memahami materi himpunan, fungsi, polinomial, dan matriks (sangat ditekankan)
2. Memahami prinsip logika matematika (konjungsi, disjungsi, implikasi, biimplikasi, ekuivalensi).
3. Dapat mereduksi matriks menggunakan Operasi Baris Elementer (OBE).

Ruang Vektor Tujuan:

1. Mengingat kembali persamaan garis dan bidang di ruang.

2. Memahami aksioma ruang vektor, kombinasi linier dan ruang bagian.

3. Mengingat kembali pengertian bebas dan bergantung linier, basis dan dimensi.

Arti geometris dari determinan:

Jika A matriks 2x2, |det(A)| = area dari jajaran genjang dibentuk oleh 2 vektor. Jika A matriks 3x3, |det(A)| = volume dari parallepipedum dibentuk oleh 3 vektor.

Persamaan garis dan bidang di ruang Garis di ruang dimensi 2:

persamaannya adalah y –a = m (x – b) (jadi diperlukan kemiringan m dan titik yang dilalui (a,b))

Bidang di ruang dimensi 3: Diperlukan inklinasi (kemiringan) dan titik yang dilalui. Untuk menyatakan inklinasi adalah satu vektor yang tegak lurus terhadap bidang.

Definisi Ruang Vektor (Vector Space)

Anggap $V$ adalah sembarang himpunan tak kosong dari objek di mana operasipenjumlahan dan operasi perkalian skalar didefinisikan. Penjumlahan yang dimaksud adalah aturan yang menghubungkan setiap pasangan objek $\overline{u} ,\overline{v}\in V$ dengan suatu objek $\overline{u} + \overline{v}$ , yang disebut sebagai jumlah dari $\overline{u}$ dan $\overline{v}$ . Sedangkan perkalian skalar adalah aturan yang menghubungkan setiap skalar $k$ dan objek $\overline{u} \in V$ dengan objek $k\overline{u}$ . Jika 10 aksioma berikut terpenuhi oleh semua objek $\overline{u} ,\overline{v} , \overline{w} \in V$ dan skalar $k$ dan $m$ , maka $V$ disebut sebagai ruang vektor dan semua objek di dalamnya disebut vektor.

Aksioma 1:
Jika $\overline{u}$ dan $\overline{v}$ adalah objek dalam $V$ , maka $\overline{u} + \overline{v}$ juga berada dalam $V$ .
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat ketertutupan operasipenjumlahan.

Aksioma 2:
$\overline{u} + \overline{v} = \overline{v} + \overline{u}$
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat komutatifpenjumlahan.

Aksioma 3:
$\overline{u} + (\overline{v} + \overline{w}) = (\overline{u} + \overline{v}) + \overline{w}$
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat asosiatif penjumlahan.

Aksioma 4:
Ada objek $\overline{0}$ dalam $V$ yang disebut objek nol (selanjutnya vektor nol), sedemikian sehingga berlaku

$\overline{0}+ \overline{u} = \overline{u} +\overline{0} = \overline{u}$
untuk setiap $u \in V$ .
Catatan 1: Aksioma ini mungkin telah dipandang umum sebagai bentuk identitas penjumlahan.
Catatan 2: Objek $\overline{0}$ yang disebut sebagai “identitas” tidak selalu berarti vektor nol $\overline{0} = (0,0,\cdots, 0)$ . Hal ini tergantung dari definisi operasi yang diberikan. Jika diberikanhimpunan $A$ , maka untuk $a \in A$ , haruslah berlaku
$a * \overline{0} = a$
Prinsip seperti ini sebenarnya sama dengan prinsip pada identitas penjumlahan/perkalian bilangan real, yaitu untuk $a \in \mathbb{R}$ ,
$a + 0 = a$ dan $a \times 1 = a$
Untuk itu, $0$ disebut identitas penjumlahan dan $1$ disebut identitas perkalian padabilangan real.

Aksioma 5:
Untuk setiap $\overline{u} \in V$ , ada objek $-\overline{u} \in V$ yang disebut negatif dari $\overline{u}$ sedemikian sehingga berlaku
$\overline{u} + (-\overline{u}) = (-\overline{u}) + \overline{u} = \overline{0}$
Catatan 1: Aksioma ini mungkin telah dipandang umum sebagai invers penjumlahan.
Catatan 2: $-\overline{u}$ juga tidak selalu sama dengan $-\overline{u} = (-u_1, -u_2, \cdots, -u_k)$ . Hal ini tergantung dari operasi yang diberikan. Suatu vektor dikatakan invers dari vektor yang lain jika keduanya dioperasikan menghasilkan identitas. Untuk itu, identitasnya harus terlebih dahulu diketahui.

Aksioma 6:
Jika $k$ adalah sembarang skalar dan $\overline{u}$ adalah sembarang objek dalam $V$ , maka berlaku $k\overline{u} \in V$ .
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat ketertutupan operasiperkalian.

Aksioma 7:
$k(\overline{u} + \overline{v}) = k\overline{u} + k\overline{v}$
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat distributif perkalian terhadap penjumlahan.

Aksioma 8:
$(k + m) \overline{u} = k\overline{u} + m\overline{u}$
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat distributif perkalian terhadap penjumlahan.

Aksioma 9:
$k(m\overline{u}) = (km)\overline{u}$
Catatan: Aksioma ini mungkin telah dipandang umum sebagai sifat asosiatif perkalian.

Aksioma 10:
$1\overline{u} = \overline{u}$
Catatan: Aksioma ini mungkin telah dipandang umum sebagai bentuk identitas perkalian.

Perlu diperhatikan bahwa skalar yang dimaksud di sini adalah BILANGAN (bukan vektor). Umumnya suatu kajian dibatasi hanya sampai bilangan real $\mathbb{R}$ saja, tetapi memungkinkan untuk diperluas sampai bilangan kompleks. Bilangan kompleks $\mathbb{C}$ adalah gabungan dari bilangan real dan bilangan imajiner (khayal). Bila dalam suatu kasus, tidak ada keterangan yang menyatakan jenis bilangan pada suatu skalar, maka skalar yang dimaksud itu adalah bilangan real.

Teorema Ruang Vektor

Jika $V$ adalah suatu ruang vektor, $\overline{u}$ adalah vektor dalam $V$ , dan $k$ sembarang skalar, maka

1. $\overline{0}\overline{u} = \overline{u}$

2. $k\overline{0}=\overline{0}$

3. $(-1)\overline{u} = -\overline{u}$

4. Jika $k\overline{u} = \overline{0}$ , maka $k = \overline{0}$ atau $\overline{u} = \overline{0}$

Definisi Subruang (Subspace) atau Ruang Bagian

Suatu himpunan bagian $W$ dari ruang vektor $V$ disebut subruang/ruang bagian dari $V$ jika $W$ sendiri adalah ruang vektor di bawah operasi penjumlahan dan perkalian skalar yang didefinisikan pada $V$ .

Teorema 1: Subruang

Jika $Q$ adalah subruang dari $P$ , maka $Q$ harus memenuhi 2 syarat berikut.

a) Jika $A, B \in Q$ , maka $A + B \in Q$

b) Jika $k$ sembarang skalar dan $A$ vektor sembarang dalam $Q$ , maka $kA \in Q$

Teorema 2: Subruang

Jika $A\overline{x} = \overline{0}$ adalah suatu sistem linear homogen dari $m$ persamaan dan $n$ variabel, maka himpunan vektor penyelesaiannya adalah suatu subruang dari $\mathbb{R}^n$ .

Catatan: Sistem linear homogen adalah sistem persamaan linear dengan konstanta 0 (nol), misalnya

$\begin{cases} 2x + 3y = 0 \\ x - 4y = 0 \end{cases}$

Notasi $\mathbb{R}^n$ (dibaca: R n, bukan R pangkat n) menyatakan ruang dimensi $n$ .

Definisi Kombinasi Linear

Suatu vektor $\overline{w}$ disebut kombinasi linear dari vektor-vektor $\overline{v}_1, \overline{v}_2,\cdots, \overline{v}_r$ jika dapat dinyatakan dalam bentuk
$\overline{w} = k_1\overline{v}_1 + k_2\overline{v}_2 + \cdots + k_r\overline{v}_r$
dengan $k_1,k_2,\cdots, k_r$ sembarang skalar.

Teorema: Hubungan Subruang dan Kombinasi Linear

Jika $\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r$ adalah vektor-vektor dalam ruang vektor $V$ , maka
a) Himpunan $W$ yang anggotanya merupakan vektor kombinasi linear dari $\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r$ merupakan subruang dari $V$ .
b) $W$ adalah subruang terkecil dari $V$ yang berisi $\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r$ dalam pengertian bahwa setiap subruang lain dari $V$ yang berisi $\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r$ pasti mengandung $W$ .

Definisi Ruang Terentang (Spanning Space)

Jika $S = \{\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r\}$ adalah himpunan vektor dalam ruang vektor $V$ , maka subruang $W$ dari $V$ yang mengandung semua kombinasi linear dari vektor dalam $S$ disebut ruang terentang oleh $\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r$ dan kita katakan bahwa $\overline{v}_1, \overline{v}_2,\cdots, \overline{v}_r$ adalah rentang $W$ . Untuk menunjukkan bahwa $W$ adalah ruang terentang oleh vektor dalam himpunan $S$ , kita tuliskan
$W = \text{rent}(S)$
atau
$W = \text{rent}\{\overline{v_1}, \overline{v}_2,\cdots, \overline{v}_r\}$
Notasi ini hanya berlaku dalam bahasa Indonesia, sedangkan secara luas (internasional) , notasi rentang disimbolkan dengan
$W = \text{span}(S)$
Untuk itu, notasi terakhir ini yang akan dipakai pada uraian selanjutnya.
Catatan: Merentang (spanning) dapat diartikan memanjang, melebar, meluas, dan sebagainya.

Teorema Rentang (Spanning)

Jika $S = \{\overline{v}_1,\overline{v}_2, \cdots, \overline{v}_r\}$ dan $S' = \{\overline{w}_1, \overline{w}_1, \cdots, \overline{w}_r\}$ adalah dua himpunan vektor dalam ruang vektor $V$ , maka
$\text{span}\{\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r\} = \text{span}\{\overline{w}_1,\overline{w}_2,\cdots, \overline{w}_r\}$
jika dan hanya jika setiap vektor dalam $S$ adalah kombinasi linear dari vektor dalam $S'$ , begitu juga sebaliknya.

Definisi Kebebasan Linear

Jika $S = \{\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r\}$ adalah himpunan vektor tak kosong, maka persamaan vektor
$k_1\overline{v}_1+k_2\overline{v}_2 + \cdots + k_r\overline{v}_r = 0$
mempunyai setidaknya satu penyelesaian, yaitu
$k_1 = k_2 = \cdots = k_r = 0$
Jika ini adalah satu-satunya penyelesaian, maka $S$ disebut himpunan yang bebas linear (linearly independent). Jika ada penyelesaian lain, maka $S$ disebut himpunan yang tidak bebas linear (atau diistilahkan, bergantung linear (linearly dependent)).

Salah satu istilah baru dari definisi ini adalah penyelesaian trivial (trivial solution), yaitu penyelesaian dari suatu sistem linear yang nilai-nilai variabelnya adalah 0.

Teorema 1: Kebebasan Linear

Suatu himpunan dengan dua atau lebih vektor disebut
a) tak bebas secara linear jika dan hanya jika paling tidak salah satu vektor dalam $S$ dapat dinyatakan sebagai suatu kombinasi linear dari vektor lainnya dalam $S$ .
b) bebas secara linear jika dan hanya jika tidak ada vektor dalam $S$ yang dapat dinyatakan sebagai kombinasi linear dari vektor lainnya dalam $S$ .

Teorema 2: Kebebasan Linear

a) Suatu himpunan vektor berhingga yang berisi vektor nol tak bebas linear.
b) Suatu himpunan dengan tepat 2 vektor dikatakan bebas linear jika dan hanya jika vektor yang satu bukan merupakan penggandaan skalar dari vektor yang lain.

Intepretasi Geometrik dari Kebebasan Linear

Dalam $\mathbb{R}^2$ atau $\mathbb{R}^3$ (ruang dimensi 2 atau ruang dimensi 3), kebebasan linear dapat dijelaskan dengan konsep geometri.

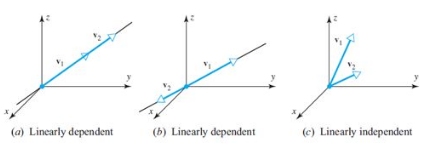
Pada $\mathbb{R}^2$ maupun $\mathbb{R}^3$ , suatu himpunan dua vektor bebas linear jika dan hanya jika vektor-vektor tersebut tidak terletak pada garis yang sama bila kedua titik pangkalnya ditempatkan pada titik asal (titik (0,0)),

sedangkan pada $\mathbb{R}^3$ , suatu himpunan tiga vektor bebas linear jika dan hanya jika vektor-vektor tersebut tidak terletak pada bidang yang sama bila ketiga titik pangkalnya ditempatkan di titik asal.

Teorema 3: Kebebasan Linear

Misalkan $S = \{\overline{v}_1,\overline{v}_2, \cdots, \overline{v}_r\}$ adalah himpunan vektor dalam $\mathbb{R}^n$ . Jika $r > n$ , maka $S$ tidak bebas linear.

Definisi Basis dalam Ruang Vektor

Jika $V$ adalah sembarang ruang vektor dan $S = \{\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r\}$ adalah himpunanvektor dalam $V$ , maka $S$ disebut basis untuk $V$ jika dua syarat berikut terpenuhi.
a) $S$ bebas linear,
b) $S$ merentang dalam $V$ .

Teorema Basis dalam Ruang Vektor

Jika $S = \{\overline{v}_1,\overline{v}_2, \cdots, \overline{v}_r\}$ adalah suatu basis untuk ruang vektor $V$ , maka setiap vektor $\overline{v}$ dalam $V$ dapat dinyatakan dalam bentuk $c_1\overline{v}_1 + c_2\overline{v}_2 + \cdots + c_r\overline{v}_r = \overline{0}$
hanya dalam satu cara.

Definisi 1: Dimensi

Suatu ruang vektor tak nol $V$ disebut berdimensi terhingga jika $V$ berisi suatuhimpunan vektor terhingga $\{\overline{v}_1,\overline{v}_2, \cdots, \overline{v}_r\}$ yang membentuk suatu basis. Jika tidak adahimpunan yang demikian, maka $V$ disebut berdimensi tak terhingga. Selain itu, didefinisikan ruang vektor nol sebagai dimensi terhingga.

Teorema 1: Dimensi

Jika $V$ adalah ruang vektor berdimensi terhingga dan $\{\overline{v}_1,\overline{v}_2, \cdots, \overline{v}_r\}$ adalah sembarang basis, maka
a) Setiap himpunan dengan lebih dari $r$ vektor tak bebas linear.
b) Tidak ada himpunan dengan vektor kurang dari $r$ yang merentang $V$ .

Teorema 2: Dimensi

Semua basis untuk suatu ruang vektor berdimensi terhingga mempunyai jumlah vektor yang sama.

Definisi 2: Dimensi

Dimensi ruang vektor berdimensi terhingga $V$ , yang dinyatakan dalam notasi $\text{dim}(V)$ , didefinisikan sebagai jumlah vektor dalam suatu basis untuk $V$ . Selain itu, didefinisikan juga bahwa ruang vektor nol mempunyai dimensi $0$ .

DEFENISI : RUANG BARIS, RUANG KOLOM, DAN RUANG NOL

Jika $A$ adalah matriks berordo $m \times n$ , maka subruang dari $\mathbb{R}^n$ yang terentang oleh vektor-vektor baris dari $A$ disebut ruang baris dari $A$ dan subruang dari $\mathbb{R}^m$ yang terentang oleh vektor-vektor kolom dari $A$ disebut ruang kolom dari $A$ . Ruang penyelesaian dari sistem persamaan homogen $A\overline{x} = \overline{0}$ yang merupakan subruang dari $\mathbb{R}^n$ disebut ruang nol dari $A$ .

TEOREMA 1 : RUANG KOLOM

Suatu SPL $A\overline{x} = \overline{b}$ konsisten (memiliki penyelesaian) jika dan hanya jika $\overline{b}$ berada dalam ruang kolom dari $A$

TEOREMA : HUBUNGAN ANTARA RUANG PENYELESAIAN $A\overline{x} = \overline{0}$

Jika $x_0$ menyatakan sembarang penyelesaian tunggal dari suatu sistem linear tak homogen yang konsisten, yaitu $A\overline{x} = \overline{b}$ , dan jika $\{\overline{v}_1,\overline{v}_2,\cdots, \overline{v}_r\}$ membentuk suatu basis untuk ruang nol dari $A$ (ruang penyelesaian dari sistem homogen $A\overline{x} = \overline{0}$ ), maka setiap penyelesaian dari $A\overline{x} = \overline{b}$ dapat dinyatakan dalam bentuk
$\overline{x} = \overline{x} _0 + c_1\overline{v}_1 + c_2\overline{v}_2 + \cdots + c_r\overline{v}_r$
dan sebaliknya dengan skalar $c_1, c_2, \cdots, c_r$ , sedangkan vektor $\overline{x}$ dalam rumus ini merupakan penyelesaian dari $A\overline{x} = \overline{b}$

Naomi Artama Silitonga

Jumat, 21 Desember 2018

RUANG VEKTOR

Tidak ada komentar:

Posting Komentar