LIMIT KONTINUITAS

KEKONTINUAN FUNGSI

Oktober 7th, 2016

 

Salah satu topik yang berkaitan dengan konsep limit fungsi adalah kekontinuan fungsi atau kontinuitas fungsi. Suatu fungsi dapat kontinu atau tidak kontinu di suatu titik.

Definisi

Misalkan f adalah suatu fungsi riil.  f dikatakan kontinu di x = c apabila:

Catatan:

Fungsi riil adalah fungsi dengan daerah asal maupun daerah nilainya merupakan himpunan bagian dari ℝ.

Persyaratan

pada definisi di atas, teknis pembuktiannya mencakup tiga hal, yaitu

Pertama, limit tersebut ada. Artinya:

Kedua, f(c) terdefinisi

Ketiga,

Apabila ada di antara ketiga hal ini yang tidak dipenuhi, maka kita simpulkan f tidak kontinu (=diskontinu) di x= c.

Contoh 1

Misalkan f suatu fungsi dari ℝ ke ℝ dengan aturan fungsi sebagai berikut.

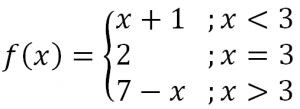
Apakah f kontinu di x = 3?

Jawab:

Langkah 1: Memeriksa eksistensi limit fungsi di x = 3

Limit kiri:

Limit kanan:

Ternyata nilai limit kirinya sama dengan limit kanannya, yaitu 4.

Kita simpulkan

dan

Langkah 2: Memeriksa apakah f terdefinisi di x = 3

Dari pendefinisian f, f(3) terdefinisi, yaitu f(3) = 2

Langkah 3: Memeriksa kesamaan nilai limit fungsi dengan nilai fungsinya

Dari langkah-langkah sebelumnya diperoleh bahwa

Kesimpulan:  f tidak kontinu (atau diskontinu) di x = 3. Situasi pada contoh ini dapat dilihat pada Gambar 1.

Gambar 1

Catatan:

Diskontinuitas di x = 3 pada Contoh 1 dinamakan ketidakkontinuan yang dapat dihapuskan. Dengan mendefinisikan kembali nilai f di x = 3, fungsi tersebut menjadi kontinu. Jadi, agar f kontinu di x = 3, kita definisikan f(3) = 4.

Contoh 2

Misalkan g suatu fungsi dari ℝ ke ℝ dengan aturan fungsi sebagai berikut.

Apakah g kontinu di x = 0?

Jawab:

Langkah 1: Memeriksa eksistensi limit fungsi di x = 0

Limit kiri:

Limit kanan:

Ternyata nilai limit kirinya tidak sama dengan limit kanannya, sehingga kita simpulkan:

tidak ada. Pada langkah ini juga, langsung simpulkan g tidak kontinu di x = 0. Situasi pada contoh ini dapat dilihat pada Gambar 2.

Gambar 2

Catatan:

Diskontinuitas di x = 0 pada Contoh 2 dinamakan ketidakkontinuan yang dapat tak terhapuskan. Kita tidak dapat mendefinisikan kembali nilai g di x = 0 untuk membuat g kontinu di sana.